Таблица умножения базисных элементов центра алгебры CS3.

Запишем матрицы C(i):

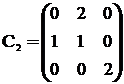; ; . (24)

Эти матрицы получаются так. Например, действие элемента С(2) на остальные элементы можно представить следующим образом:

;

;

.

Записывая коэффициенты правой части в столбец, получаем С(2).

Мы построили матричное представление базисных элементов центра Z алгебры CS3, что позволяет получить и матричное представление центра этой алгебры.

Запишем характеристические уравнения для определения собственных чисел и собственных векторов матриц Ci в следующем виде (рассматриваем сначала общий случай d матриц Ci):

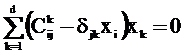. (25)

Возвращаясь к случаю группы S3 получаем d=3, а коэффициенты можно найти из табл. 4 на основании выражения (24). При этом сначала зафиксируем индекс j, а индексы i и k будем менять, что позволяет разбить систему (25) на три подсистемы, соответствующие значениям j=1, 2, 3. Выпишем сначала 27 значений Cijk, разбитых на три группы, по 9 значений в каждой:

С111=1; С112=0; С113=0;

С211=0; С212=1; С213=0;

С311=0; С312=0; С313=1;

С121=0; С122=1; С123=0;

С221=2; С222=1; С223=0; (26)

С321=0; С322=0; С323=2;

С131=0; С132=0; С133=1;

С231=0; С232=0; С233=2;

С331=3; С332=3; С333=0;

Тогда находим следующие системы уравнений:

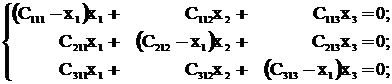
(27)

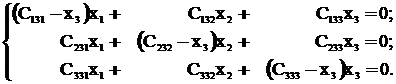
Подставляя в найденные системы уравнений (27) значения из выражений (26), получим

(1-х1) х1=0; - х2 х1+ х2=0; - х3 х1+ х3=0;

(1-х1) х2=0; (I) 2х1+(1-х2) х2=0; (II) - х2 х3+2х3=0; (III) (28)

(1-х1) х3=0; (1-х2) х3=0; 3х1+3х2-x32=0.

Обратим внимание на два обстоятельства.

1. Во всех трех системах находятся одни и те же неизвестные, стоящие вторыми сомножителями, т. е. вектор x=(x1, x2, x3) является общим собственным вектором всех матриц С(1), С(2), С(3).

2. Указанные системы можно получить, взяв матрицы (24), транспонировать их, рассмотреть разности C(1)-X1E, C(2)-X2E, C(3)-X3E и затем умножить полученные матрицы на столбец (x1, x2, x3)Т (знак Т обозначает транспонирование).

Заметим, что выше уже записаны уравнения для нахождения собственных векторов матриц C(i), однако в этих уравнениях фигурируют собственные значения этих матриц, которые необходимо найти. Для матрицы С(1) получаем трехкратное собственное значение, равное единице, поэтому находим собственные значения матриц С(2) и С(3). Запишем для них вековые уравнения: