1. На примере группы C3V покажем некоторые приемы и соображения, с помощью которых можно составить таблицу характеров неприводимых представлений. Характер тождественного представления c1(А1) записывается сразу.

Для составления характера c2(А2) воспользуемся перестановочным представлением S3 группы C3V. Подстановки, соответствующие элементам , , =1 – четные, остальные подстановки – нечетные. Так как произведение четных подстановок – четная подстановка, причем четные подстановки образуют подгруппу А3 группы S3, то четным подстановкам сопоставим число 1, а нечетным – число –1. Произведение нечетных подстановок – четная подстановка и (-1)(-1)=1, а произведение подстановок разной четности – нечетная подстановка и (-1)1=1(-1)=-1. Следовательно, мы получили одномерное представление группы C3V, в котором элементам 1, , сопоставляется 1 (эти элементы представляются четными подстановками), а остальным элементам , , сопоставляется –1 (или соответствуют нечетные подстановки). Так как одномерные представления совпадают с характерами, то получаем вторую строку таблицы. Третья строка таблицы получается из следующих соображений. В теории представлений группы известно, что число неприводимых представлений группы равно числу классов сопряженных элементов. Поэтому группа C3V имеет три неприводимых представления. Известно также, что сумма квадратов размерностей неприводимых представлений равна порядку группы. В рассматриваемом случае 12+12+Z2=6, т. е. Z=2. Следовательно, группа C3V имеет двумерное неприводимое представление, в котором

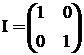, т. е. c(1)=2 (см. табл. 2).

Остальные элементы строки c3 получаются из соотношений ортогональности для неприводимых представлений: и , где x, y – неизвестные числа из строки c3. Отсюда 2х+3y=-2, 2x-3y=-2, т. е. х=-1, y=0. Мы построили таблицу характеров неприводимых представлений, не зная двумерного неприводимого представления группы C3V.

2. Нахождение характеров неприводимых представлений группы S3.

Проиллюстрируем алгоритм нахождения характеров на примере групп S3.

Необходимо разложить все перестановки группы в произведении циклов. Элементы одинакового циклического строения образуют классы. Выпишем все перестановки группы S3:

; ; ; ;

; .

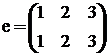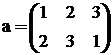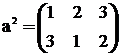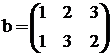При записи перестановок в циклах, если элемент i переходит в k, то k стоит не под i, а рядом с i; при этом цикле длины 1, кроме e=(1), не пишутся. Таким образом, в циклах e=(1); a=(1 2 3); a2=(1 3 2); b=(2 3); c=(1 3); d=(1 2).

В такой записи наглядно видно циклическое строение группы. Поэтому сразу находим все три класса сопряженных элементов группы S3:

K1={(1)}; K2={(1 2 3), (1 3 2)}; K3={(2 3), (1 2), (1 3)}.

Групповая алгебра CS3 группы S3 состоит из элементов

a=a1e+a2a+a3a2+a4b+a5c+a6d, (23)

где aiÎC; e, a, a2, b, c, d – шесть перестановок, образующих группу S3. Учитывая обозначения перестановок, запишем элементы групповой алгебры, являющиеся суммами элементов классов: