Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера
Материалы / Теория симметрии молекул / Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера
Страница 2

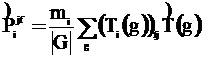. (40)

Из соотношений ортогональности для матриц неприводимых представлений следует, что этот оператор дает возможность получить eigs по формуле

, i=1, 2, …, t. (41)

Все сказанное можно выразить в виде следующего алгоритма.

Для того, чтобы найти базу модуля М из элементов, преобразующихся по неприводимым представлениям Тi, содержащихся в представлении Т, связанном с модулем М, необходимо:

1.По формуле (32) найти размерности подпространств Мij, соответствующих j-компоненте неприводимого представления Ti.

2.Найти с помощью оператора проектирования (39) все подпространства Mij.

3.В каждом подпространстве Mij выбрать произвольную ортонормированную базу.

4.Используя формулу (41), найти все элементы базы, преобразующихся по остальным компонентам неприводимого представления Тi.

Страницы: 1 2 

Смотрите также

Обработка резанием.
Обработка резанием является универсальным методом размерной обра­ботки. Метод позволяет обрабатывать поверхности деталей различной формы и размеров с высокой точностью из наиболее используемых конс ...

Степень набухания целлюлозы в растворах щелочей
При действии на целлюлозу растворов щелочей происходят как структурные и химические ее изменения, так и физико-химические процессы. Последние приводят к интенсивному набуханию целлюлозы и к ...

Медь
Медь в латинском языке — Cuprum. Это один из известнейших химических элементов, этот металл известен с глубокой древности. По данным археологической науки медь была хорошо известна егип ...