Сложный технологический процесс можно рассматривать как многомерный объект, на который действуют вектор входных параметров X и вектор управления Z. Выходные параметры составляют вектор выходных параметров Y. Общий вид статистической модели такого объекта в векторной форме

Y=f(X,Z). (9)

Для построения статистической модели абсорберов по данным таблицы 2 использовался метод Брандона (см. Приложение 2).

Сущность метода заключается в следующем. Предполагается, что функция F(x1,x2,…,xm) в формуле (9) является произведением функций от входных параметров, т.е.

, (10)

где yрi – расчетное значение i –го выходного параметра;

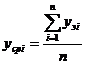- средняя величина экспериментальных значений i – го выход-ного параметра;

n – количество опытов в исходной выборке.

При использовании метода Брандона важен порядок следования функций в уравнении (10). Чем больше влияние оказывает фактор на выходной параметр, тем меньшим должен быть его порядковый номер в указанном уравнении. Поэтому задача построения модели по методу Брандона разбивается на два этапа:

1. ранжирование влияющих факторов.

2. выбор вида зависимости и построение статистической модели.

Оценить степень влияния k-го фактора на выходной параметр можно по величине частного коэффициента множественной корреляции:

, (11)

где - величина частного коэффициента корреляции, учитывающая влияние k-го фактора на выходной параметр y при условии, что влияние всех прочих факторов исключено; D- определитель матрицы, построенной из парных коэффициентов корреляции. Матрица имеет вид

Dm+1,k – определитель матрицы с вычеркнутыми m+1 строкой и k-м столбцом;

Dk,k , Dm+1,m+1 – определители матриц с вычеркнутыми k-м и (m+1)-м столбцом и строкой соответственно.

Порядок расположения влияющих факторов в уравнении (10) определяют в соответствии с убыванием величины частных коэффициентов корреляции.

В уравнении (10) каждая из функций f1(x1),f2(x2),…fm(xm) принимается либо линейной, либо нелинейной (степенной, показательной, экспоненциальной и т.д.)

Перед определением вида первой зависимости следует представить исходные экспериментальные значения выходного параметра в каждом опыте yэj в безразмерной форме yэ0j :

, (12)

где yср- средняя величина выходного параметра.

Таким образом, исходными данными для поиска первой зависимости будут нормированные значения вектора выходных параметров и опытные значения первого влияющего фактора. Поиск зависимости yр1=f1(x1) может осуществляться по-разному.

Выбрав зависимость yр1=f1(x1), определяют остаточный показатель yэ1 для каждого наблюдения:

. (13)

Предполагая, что yэ1 не зависит от x1 ,а зависит от x2,…,xm , выбирают зависимость от второго фактора. Получив расчетную зависимость yр2=f2(x2 ), находят остаточный показатель yэ2 для каждого наблюдения:

. (14)

Выполнив аналогичные действия для каждого k-го влияющего фактора, получают регрессионную зависимость для рассмотренного выходного параметра. Порядок расположения факторов для этой зависимости определен на этапе ранжирования и отличается от порядка факторов в уравнении (10). Совокупность зависимостей по каждому выходному параметру представляет собой статистическую модель многомерного технологического объекта.