При наличии градиента температуры в зернистом слое, заполненном жидкостью или газом достаточно большой плотности, может возникнуть естественная конвекция, приводящая к заметному увеличению эффективного коэффициента теплопроводности.

С возможностью естественной конвекции нужно считаться при процессах горения в шахтных топках и газогенераторах, при каталитических процессах в начальных участках реакторов с большим градиентом темепратуры и концентрации, в доменных печах, в тепловой изоляции в виде зернистой засыпки.

Рассмотрим зернистый слой высотой x, имеющий температуру верхнего торца t2 и нижнего торца t1, причем t1>t2. При отсутствии конвективных потоков газа в слое установится одномерный тепловой поток q, определяемый коэффициентом теплопроводности lоэ при линейном распределении температуры по высоте слоя. Примем далее, что в направлении, одинаковом с направлением теплового потока, движется поток газа (жидкости) с массовой скоростью G; распределение температуры по высоте слоя остается неизменным и одинаковым для обеих фаз. Такое допущение оправдано, если основное количество теплоты передается теплопроводностью. Конвективный тепловой поток:

qк=СpG(t1-t2) (VI)

Конвективная составляющая коэффициента теплопроводности описывается выражением:

lк=qк/(t1-t2)/x=CpGx (VII)

а суммарная теплопроводность слоя при наличии конвекции равна:

lэ=lоэ+lк (VIII)

В рассматриваемом случае естественная конвекция в слое вызвана различием плотности газа за пределами слоя при t2 и средней плотности в слое при температуре 0.5(t1+t2).

Dr=0.5rbtDt (IX)

где bt - коэффициент объемного расширения газа; Dt=t1-t2.

Движущая сила газового потока Dp=хDrg уравновешивается в слое, который при вязкостном течении жидкости выражается зависимостью:

Из этой зависимости имеем:

где С=e3/a2K - коэффициент проницаемости слоя, зависящий от его структуры.

После некоторых преобразований получаем:

Здесь:

- критерий Грасгофа, отнесенный к разнице температур в слое; в качестве определяющего размера принята высота слоя;

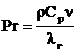
- критерий Прандтля для газовой среды;

- критерий Релея для зернистого слоя.

В отличие от аналогичного критерия GrPr, применяемого для описания естественной конвекции в однофазной среде, а Ra входят два симплекса, отражающие тепловые и гидравлические свойства зернистого слоя.

С учетом принятых обозначений:

j=1+0.5Ra (XIII)

В более общем случае, когда естественная конвекция возникает в замкнутом с торцов зернистом слое, коэффициент в формуле (XIII) должен измениться. Кроме того, нарушение устойчивости газовой среды в слое и начало естественной конвекции должно определяться некоторым критическим значением Ra0, так же, как это имеет место в однофазной среде.

В соответствии с этим формула (XIII) приобретает вид:

j=1+y(Ra-Ra0) (XIV)

Естественная конвекция в зернистом слое может возникнуть из-за различия концентрации по высоте слоя, вызывающей различие плотностей газа. В этом случае критерий Gr заменяется критерием Архимеда: