2.3.1. Эволюция системы определяется, с одной стороны, ее мгновенным состоянием и, следовательно, волновой функцией. С другой стороны, изменение состояния во времени зависит от "скорости" эволюции, т.е. от производной волновой функции по времени. Вместе с тем такое изменение связано с каким-либо взаимодействием с окружающими систему объектами и, следовательно, с обменом энергией. Это означает, что при описании эволюции необходимо связать саму волновую функцию, ее производную по времени и гамильтониан, в общем случае зависящий от координат и времени.

2.3.2. Такая связь вводится в виде временнớго уравнения Шрёдингера, которое является одним из постулатов квантовой механики и записывается в форме:

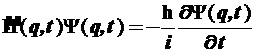(2.19)

Возможные функции состояния системы удовлетворяют уравнению (2.19)

2.3.3. В том случае, когда гамильтониан Н, а, следовательно, и энергия системы не зависят от времени, временное уравнение Шредингера легко преобразуется в стационарное уравнение Шредингера, имеющее структуру операторного уравнения (1.1).

Произведем соответствующие преобразования. Для этого положим, что гамильтониан не включает времени в явном виде и зависит только от координат

(2.20.)

Это позволяет нам использовать метод Фурье для разделения переменных и представить волновую функцию в виде двух сомножителей, одного покоординатного и другого временного:

(2.21)

Подставим результат в (2.20) и перенесем влево от , а влево от оператора дифференцирования по времени, так как по отношению к этим операторам выносимые множители условно постоянны и не преобразуются:

,

(2.22)

Теперь разделим переменные в уравнении (2.22)

(2.23)

С учетом независимости пространственных и временных переменных следует обе части полученного равенства (2.23) приравнять одной и той же постоянной величине, в результате получим систему из двух уравнений:

(2.24)

(2.25)

Легко видеть, что выражение (2.25) имеет вид операторного уравнения (1.1) и, следовательно, постоянная const есть собственное значение гамильтониана, то есть энергия системы:.

Временная часть волновой функции φ(t), получаемая как решение уравнения (2.24), имеет вид строго периодического процесса, совершающеюся с круговой частотой, а именно:

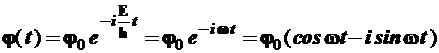(2.26)

Как уже говорилось ранее, временная периодичность функций состояния является неотъемлемой чертой стационарного движения. Операция комплексного сопря­жения уравнения (2.19) означает замену t на -t, т.е. время как бы обраща­ется вспять. Временная часть волновой функции в (2.26) обратится в физически эквивалентную , но любая наблюдаемая величина останется той же самой согласно (1.5). Уравнение Шрёдингера описывает, таким образом, процессы, обратимые во времени.

2.3.5.

Наконец, из уравнения (1.25) для стационарных систем получаем операторное выражение закона сохранения энергии:

(2.27)

Это выражение называется стационарным уравнением Шрёдингера. Оно не содержит времени в явном виде. Стационарное уравнение Шрёдингера является основным инструментом для решения теоретических задач об электронном строении атомно-молекулярных систем. В процессе точного или приближенного решения уравнения (2.27) находится вид волновой функции, а также энергия исследуемых состояний.

2.3.6. Всякая система характеризуется своим гамильтонианом, и он является тем исходным общим условием, которое управляет и характером движения, и предписывает возможный вид состояний и уровней системы